SSB蓄电池研讨体系的描绘

2026-02-05 09:01:32

1研讨体系的描绘

图1展现了所提出体系的装备，该体系运用了一个集中式PMS管理器。它由一个光伏发电器和电池组组成，经过直流/直流升压变换器连接到直流母线，其间光伏发电器的变换器为单向，电池的变换器为双向；后者保证了这些电池以及与直流母线相连的柴油发电机（经过无控整流器（沟通/直流）后接直流/直流升压变换器）的充电和放电操控。这是一个非并网体系，具有直流母线结构，用于给孤立的沟通负载供电，经过直流/沟通逆变器模仿家庭用电。

Fig. 1:

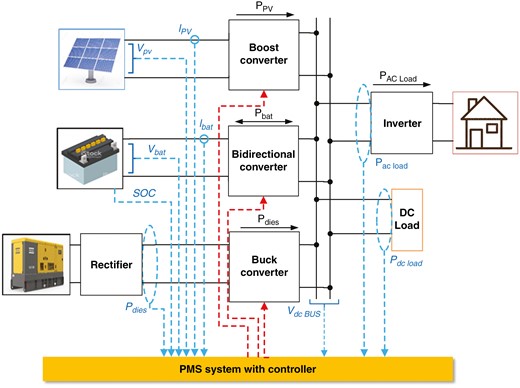
所提出的独立混合体系。

PMS体系需要保证电源之间的有用交互以完成高效的电力平衡负载，维护电池免受深度放电或过充电的影响并避免停电。依据实时监测的参数（阳光、电池充电状况和负载需求），PMS体系确认体系的运转形式，并对给定到各个调理器转换器的值做出反应，以操控每个电源的功率。

2 所提出的选用含糊逻辑操控的电源管理体系 (PMS-FLC)

对相似文献的回顾表明，在PMS范畴最具有应战性的差距是在不同的操作形式之间坚持不同动力之间的滑润过渡（例如，电池隔离当它充满电时以及当它接近深度放电状况时）[14]。

因而，这种抱负的行为供给了更好的能量平衡，并进步了动力功率。然而，在混合体系的传统PMS中，操作形式是经过忽然切换挑选的，导致瞬时改动的功率参阅[14]。这些类型的参阅大多数调理器不容易盯梢，特别是像PI（份额积分）操控器这样的常规调理器[14]。此外，它们还会引起瞬态体系，影响体系的稳定性和最小化其功率。为了应对这一应战，将FLC引入PMS结构似乎是一个有用的解决计划，能够经过在它们之间引入一个中间阶段来保证不同形式之间的滑润和灵敏切换。PMS-FLC依照以下约好规划并装备为缩放一切预期的体系场景：

• 为负载供电所挑选的数据源按优先级排序；光伏发电被认为是主要数据源，其次是电池储能，最终是柴油发电机。

• 电池充电仅经过运用光伏发电机产生的多余电力进行。

• 柴油发电机仅在电池放电且光伏发电机的电力缺乏时才会启动。

2.1 光伏体系操控

光伏发电器有两种操作形式。第一种形式是MPPT形式，在此形式下，光伏发电器供给最大功率以满意负载需求。在能量过剩时，如果电池没有充满（SOC ≤ SOCmax），光伏发电器将被重新定向为电池充电。另一种形式是LPP形式，在这种形式下，电池已充满电，光伏发电器的角色仅限于满意负载需求[11, 12]。

为了保证光伏发电机的两种运转形式，该发电机有必要连接到直流/直流变换器，该变换器被视为直流母线和该发电机之间的阻抗适配器，能够改动其作业点以盯梢PMS-FLC体系施加的参阅点。

图2a所示依据PMS-FLC的光伏体系操控有三个输入：

Fig. 2:

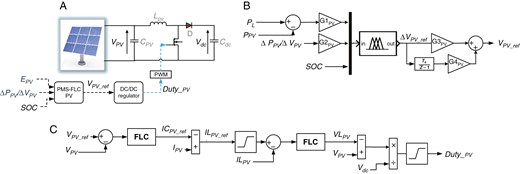
光伏发电操控系。（a）大局计划，（b）PMS-FLC光伏体系，（c）直流/直流调理器。

• 负载恳求的功率与光伏发电器供给的功率之间的差错（E_PV）；这个输入用于在LPP形式下操控体系。

• 光伏发电体系功率改动与电压改动之比（∆P PV /∆V PV）；该输入用于确认光伏发电体系的运转点，以操控体系在最大功率盯梢形式或线性功率形式下作业。

• 电池的SOC；这个输入是用来在LPP和MPPT两种形式之间进行挑选的。实际上，有三个提议的SOC水平：低SOC是电池到达深度放电的水平；高SOC是电池处于完全充电状况的水平；中等水平介于这两个前两个水平之间。依据这三个水平，PMS-FLC挑选PV的操作形式，如表1所示。

依据SOC水平的PV形式挑选

SOC = 低 .	SOC = 中等	SOC = 高 .
最大功率点盯梢形式	最大功率点盯梢形式	低功耗形式

如图2b所示，PMS-FLC运用上述三个输入来给出一个单一的输出，该输出表明所需的PV发电机输出电压。这个参阅电压将用作直流/直流变换器调理器的输入。

该调理器选用两级级联结构，装备含糊逻辑操控器，旨在经过脉冲宽度调制模块生成适当的占空比，从而产生开关信号，如图2c所示。其间，\(I_{C_{PV_{ref}}}\) 和 \(I_{L_{PV_{ref}}}\) 别离是电容 \(C_{PV}\) 和电感 \(L_{PV}\) 的参阅电流；依据第一个含糊逻辑调理器，\(I_{L_{PV}}\) 和 \(V_{L_{PV}}\) 别离是电感 \(L_{PV}\) 的电流和电压；而 \(duty_{PV}\) 是光伏发电机的直流/直流变换器的占空比。

       在图2b中，负载和光伏功率之间的差错为 EPV=PL−PPV，其间 PL=ILoadVdc 和 PPV=IPVVpv，其间 Vdc 和 Vpv 别离表明直流母线电压和光伏电压，ILoad 和 IPV 别离表明负载电流和光伏电流。光伏功率的改动为 ∆PPV=PPV(K)−PPV(K−1)，光伏电压的改动为 ∆Vpv=Vpv(K)−Vpv(K−1)。光伏参阅电压的改动为 ∆Vpv_ref=Vpv_ref(K)−Vpv_ref(K−1)，其间 Vpv_ref 表明光伏输出参阅电压。

2.1.1 MPPT形式

这种形式适用于电池未充满电的状况，此韶光伏发电机会在负载水平无关的状况下供给最大功率。最大功率点（MPP）坐落光伏的功率曲线的顶部。如果光伏功率在MPP的左边，即（∆P PV /∆V PV ）为正，则有必要增加 V PV_ref 以到达MPP；否则，有必要削减 V PV_ref 。

文献中提出了多种完成最大功率点盯梢(MPPT)的办法[21]，其间最好的办法是那些在寻觅最大功率点时具有可变步长(∆V PV_ref)的办法，这样可以削减呼应时间和低纹波，从而进步光伏发电器的运用功率[21-23]。本节介绍的MPPT依据具有可变步长(V PV_ref)的含糊逻辑。这种办法具有几个优点，例如更好的功能、鲁棒性和简略性[21-23]。图3显示了用于MPPT输入和输出的七个三角 Membership Functions (MFs)，表2指出了MPPT的规矩基础。输入E PV、(∆P PV/∆V PV)和输出(∆V PV_ref)被划分为七个含糊调集：NB（负大）、NM（负中）、NS（负小）、Z（零）、PS（正小）、PM（正中）和PB（正大）。

MPPT形式和LPP形式的规矩基础

形式	MPPT形式（SOC = Z或SOC = PS）							LPP形式（SOC = PB）
"E PV ∆P PV / ∆V PV . "翻译成中文是：“E PV ∆P PV / ∆V PV . ”这儿没有改动原文的意义和格式。 PV	NB .	NM .	NS .	Z .	PS .	下午	PB .	NB .	NM .	NS .	Z .	PS .	下午	PB .
NB	NB	NB	NB	NB	NB	NB	NB	PB	下午	PS	Z	NS	纳米	NB
纳米	纳米	纳米	纳米	纳米	纳米	纳米	纳米	PB	下午	PS	Z	NS	纳米	纳米
NS	NS	NS	NS	NS	NS	NS	NS	PB	下午	PS	Z	NS	NS	NS
Z	Z	Z	Z	Z	Z	Z	Z	NB	纳米	NS	Z	Z	Z	Z
PS	PS	PS	PS	PS	PS	PS	PS	PS	PS	PS	PS	PS	PS	PS

Fig. 3:

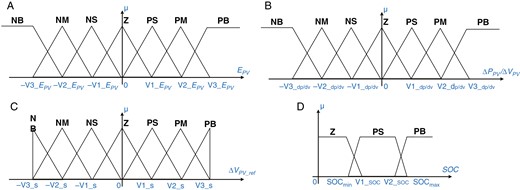
输入和输出含糊集。(a) EPV，(b) ∆PPV/∆VPV，(c) ∆VPV_ref，(d) SOC。

2.1.2 LPP形式

该形式在电池充满电时（SOC = 高）执行；因而，光伏发电机的功率等于负载恳求的功率。在这种状况下，调理器运用输入（∆P PV /∆V PV ）来确认光伏发电机的当时作业点，并运用输入 E PV 来消除差错。PMS-FLC 运用表 2 中说到的规矩库来供给输出 V PV_ref。因而，它保证在（∆P PV /∆V PV ）为负的一侧进行调理，如图 4 所示。

Fig. 4:

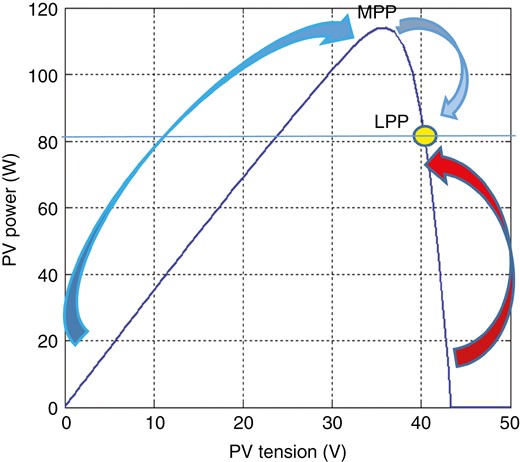
限制光伏发电机的运转形式。

2.1.3 光伏发电机的PMS-FLC

如前所述，应用于光伏体系的PMS-FLC保证了其作业形式，并依据电池的SOC挑选合适的运转形式，如表2所示。在这种状况下，SOC输入被划分为三个含糊调集：Z（SOC=低）、PS（SOC=中）和PB（SOC=高）。相应的MF如图3d所示。另外两个输入和输出坚持与之前界说的一致。

2.1.4 依据PSO的办法来确认优化的MF设置和增益值

所提出的PMS-FLC体系的功能与FLC参数的正确挑选密切相关，特别是MF参数，例如图3中给出的MF值（V1，V2，V3）以及图2b中显示的四个增益值G1到G4。为了处理这些大量的未知数，选用了一种依据PSO算法的高效办法，因为其在解决复杂的优化问题时既简略又高效[24]。

PSO是一种受一群鸟或鱼的行为启发的启发式优化办法；它最早由Eberhart和Kennedy于1995年开发[25]。在这个算法中，每个粒子经过改动其速度来寻觅查找空间周围的最佳解决计划，依据其当时方位、自身最佳解决计划和大局最佳解决计划。这种改动将使其新的方位收敛到最佳解决计划。这个操作会重复进行，直到满意某个规范停止。在规范的PSO中，粒子依据以下方程进行操作[24]：

其间 \( v_{i,t+1} \) 和 \( v_{i,t} \) 表明第 \( i \)-个粒子的当时速度和未来速度，\( x_{i,t+1} \) 和 \( x_{i,t} \) 表明第 \( i \)-个粒子的当时方位和未来方位，\( w \) 表明一个加权函数，用于操控粒子当时速度对未来速度的影响。变量 \( p_{i,d} \) 表明第 \( i \)-个粒子在第 \( t \)-次迭代时的最佳解，而 \( p_{i,g} \) 表明最佳大局解。这两个加权因子，\( c_1 \) 和 \( c_2 \)，决议了当时局部最优解和大局最优解的重要性。最终，\( r_1 \) 和 \( r_2 \) 是两个在 [0, 1] 范围内的随机数。

为了从PSO中取得最佳解决计划，其完成遵从以下步骤[20]：

• 挑选要优化的FLC参数：运用PSO优化的参数包括图3b中PV输入的MF值V1_E PV 、V2_E PV 和V3_E PV ；∆P PV /∆V PV 输入的V1_dp/dv、V2_dp/dv和V3_dp/dv；SOC输入的V1_SOC和V2_SOC；以及图3c中∆V PV_ref输出的V1_s、V2_s和V3_s，其间0 ˂ V1 ˂ V2 ˂ V3 ˂ 1，且SOC_min ˂ V1_SOC

  上一篇：SSB蓄电池统一模糊逻辑控制器及孤立住宅混合光伏/柴油/电池能源系统的电力管理

  下一篇：SSB蓄电池操控