SSB蓄电池效果与谈论

2026-02-05 09:04:47

效果与谈论

为了验证所提出的PMS-FLC的功率，所提出的系统已经在MATLAB®/SIMULINK®（Simscape Electrical TM）系统环境中进行了仿真。面板和电池的数量被选择以掩盖负载，即一所房子。每个模块的参数如表6所示，其间Pmax标明光伏最大功率，Voc,n标明开路电压，Isc,n标明短路电流，Vmp和Imp别离标明MPP电压和电流，所有这些参数都是在标准测验条件下（STC）设置的。

光伏/电池/柴油和直流/直流变换器的仿真参数

生成器	模型	直流/直流转换器
光伏发电设备	模块：三星SDI PV-MBA 1BG 250 最大功率 = 250瓦，开路电压Voc,n = 37.9伏，短路电流Isc,n = 8.85安 Vmp：30.3伏，Imp：8.24安，并联数量：4个，串联数量：3个	升压，电感 LPV = 5 毫亨，电容 CPV = 700 微法拉，频率 = 20 千赫兹
电池	型号：锂电池电压 = 24 V，容量 = 100 Ah，初始SOC  = 50%，数量：串联5个
柴油机+整流器		电感器，L = 9 毫亨，频率 = 20 千赫兹

所提出的PMS-FLC功用测验分为两个阶段进行。第一阶段涉及光伏发电机在MPPT方式或LPP方式下的功用，第二阶段则是系统在三个源（光伏、电池和柴油）之间的运转方式产生改动时的情况。

3.1 粒子群优化PMS-FLC光伏发电功用

PSO在以下条件下运用：

• 负载恳求的功率等于2000瓦。在T=25°C下，太阳辐照度从0到1000瓦/平方米的阶跃改动在t=0.1秒时进行。仿真持续时间为0.5秒，光伏发电机在[0 0.3]秒内以MPPT方式运转，在[0.3 0.5]秒内以LPP方式运转。

•     参看功率在[0.1 0.3]秒期间设置为 P ref  = P MPP = 2996.5 W，在[0.3 0.5]秒期间为 P ref =  P LPP = 2000 W，如图8所示。

图7展现了习气度函数的演化过程，它在100次迭代后抵达最小值0.857。

Fig. 7:

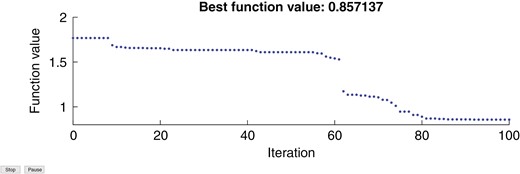
习气度函数与迭代次数对比。

表7闪现了图3中所示的PV发电机的PMS-FLC成员参数通过PSO优化的值。

运用PSO优化的隶属函数参数值

光伏输入		∆P PV /∆V PV 输入 . PV		∆V PV_ref 输出 .		收益		SOC输入
V1_E PV		V1_dp/dv		V1_s		G1 PV		SOC_ 最大值
V2_E PV		V2_dp/dv		V2_s		G2 PV		SOC_ 分钟
V3_ E PV		V3_dp/dv		V3_s		G3光伏		V1_SOC
						G4 PV		V2_SOC

图8展现了运用PSO算法的最优参数获得的效果。这些效果与运用扰动和观测（P&O）方法抵达最大功率点（MPP）或最小功率点（LPP）的经典方法所获得的效果进行了比较，如[11, 12]中所述。表8给出了每种方法的功用，其间所提出的方法在动态（减少上升时间）和静态（减少纹波）功用方面均闪现出更好的效果，然后获得了最佳的收益率。另一方面，具有较高步长（0.1V）的P&O方法闪现出良好的动态功用，且上升时间缩短。然而，静态功用因为存在高纹波而恶化。相比之下，具有较低步长（0.01V）的P&O方法减少了稳态纹波，但上升时间相应增加。这种经典技能难以在动态和静态功用方面都供给良好的功用，因而必须在它们之间进行权衡。

不同方法的功用（P&O和所提出的方法）

	最大功率点跟踪（方式）		LPP（方式）		收益率（%）
	上升时间（秒）	涟漪（W）	上升时间（秒）	涟漪（W）
P&O（步长 = 0.01 V）
P&O（步长 = 0.1 V）
提议的PMS-FLC

Fig. 8:

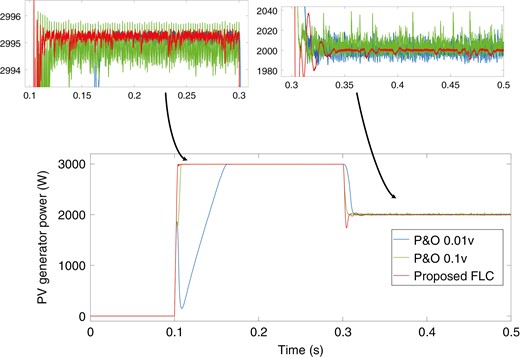
不同方法（P&O和所提出的方法）下的光伏发电功率。

表8中闪现的每种方法的产值是依据以下联络[28]核算得出的：

其间To = 0.1秒，Tf = 0.5秒，Pref和PPV别离是功率参看和光伏发电机功率。

3.2 全球系统在改动运转方式时PMS-FLC的功用

所提出的PMS-FLC将与文献[11, 12]中选用的经典方法进行比较，以管理多源混合系统。比较在以下两种情况下进行：

景象一

在最大辐照度（1000 W/m²）下，光伏发电器以MPPT方式运转，一起为负载供电并为电池充电。当电池充满电时（SOC = SOCmax），光伏发电器从MPPT方式切换到LPP方式。

景象二

在无辐照条件下，电池向固定负载供电，当其抵达深度放电状况（SOC = SOCmin）时，柴油机初步接纳为同一负载供电。

  如图9a所示，电池在t=2.5s时抵达满充状况（SOC=80%）。此刻，光伏发电机的运转方式从MPPT（PV=2996W）变为LPP（PV=200W），如图9b所示。这一改动在直流母线电压上产生了一个突然的扰动，如图9c所示。图9d承认了电池已充满电，因为其功率从-2696W变为0W。

Fig. 9:

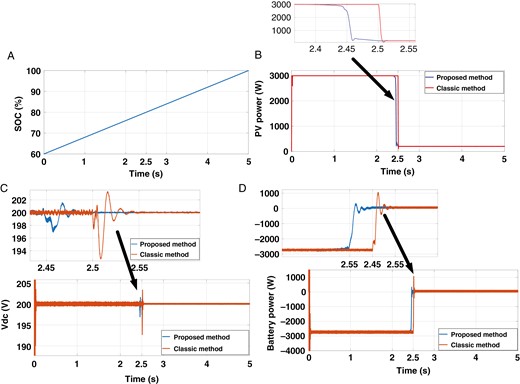
第一场景的效果。(a) 电池剩余容量（%），(b) 光伏功率，(c) 直流母线电压，(d) 电池功率。

依据突发方式改动的经典PMS会导致功率振荡和直流母线电压尖峰。当运用依据迷糊逻辑的PMS时，这些缺陷被大大下降。实际上，PMS-FLC可以下降直流母线电压（衰减2%）和电池功率扰动，并显着减少功率时间照应。这是因为所提出的PMS运用图3d中给定的SOC输入进行了软方式改动。

图10展现了履行第二个场景时的系统照应。电池初步独自为1500瓦的孤立负载供电，如图10a所示，电池在t=3秒时抵达其深度放电状况（SOC=20%）。这可以通过电池功率从1500瓦变为0瓦来体现，如图10d所示。一起，柴油机功率从0瓦增加到1500瓦，如图10b所示，满足负载需求。再次强调，依据迷糊系统的所提出的PMS确保了与经典系统相同的功率平衡，但柴油发电机功率在图10b中逐渐增加。

Fig. 10:

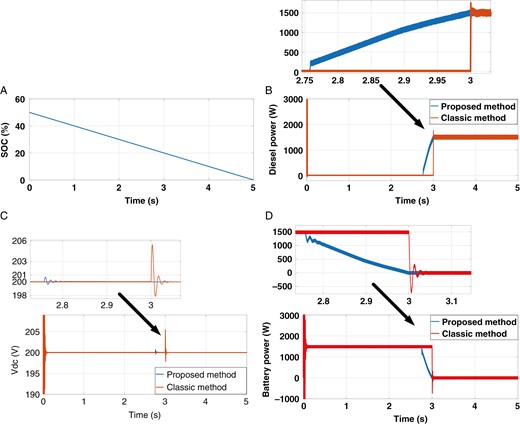
第二个场景的效果。(a) 电池剩余容量（%），(b) 柴油机功率，(c) 直流母线电压，(d) 电池功率。

通过刺进一个由SOC输入操控的中心阶段来完结平稳过渡，其 Membership Functions（MFs）如图3d所示，这导致直流母线电压的扰动更少（0.5%），如图10c所示。

4 结论

本文提出了一种依据迷糊逻辑的优化能量管理策略，以最大化混合系统（结合了光伏和柴油两种能源以及一个连接到同一直流母线并给孤立负载供电的电池储能系统）的功率。对混合系统的不同运转条件进行PMS-FLC仿真，效果闪现直流母线的稳定性极佳，且在瞬态状况下源功率的波动很小，这反映了所提出的PMS-FLC相对于运用直接过渡的传统PMS的优势，这是因为在坚持电池SOC在20%到80%之间时，光伏和柴油发电机之间的平滑切换。这提高了功用，并在改动方式时使直流母线电压超调减少了2%，一起光伏发电机的功率也提高了99.5%。

利益冲突声明

咱们承认，本出版物不存在已知的利益冲突，而且这项作业没有遭到任何或许影响其效果的严重财务支撑。